Search Trees is a data structure for storing an evolving set of objects, like a heap.
1. Sorted Arrays
Before discussing the search trees, lets discuss a little bit about sorted array.
it can do everything a sorted array can do, while also accommodating fast insertions and deletions.
Supported Operations
Search: for a key k, return a pointer to an object in the data structure with key k.
MIN (MAX): return a pointer to the object in the data structure with smallest key.
PREDECESSOR(SUCCESSOR): given a pointer to an object in the data structure, return a pointer to the object with the nect_smallest key.
OUTPUTSORTED: output the objects in the data structure one by one in order of their keys.
SELECT: given a number I, between 1 and the number of objects, return a pointer to the object in the data structure with the with-smallest key.
RANK: given a key k, return the number of objects in the data structure with key at most k.
Unsupported Operations
However, such a data structure doesn’t support INSERT and DELETE.
But it’s not definitely impossible to implement with sorted array, but they’re painfully slow.
So we are longing for a data structure which keeps the properties that search trees have, while matching the high performance of a heap for the INSERT and DELETE operations.
2. Sorted Trees: Supported Operations
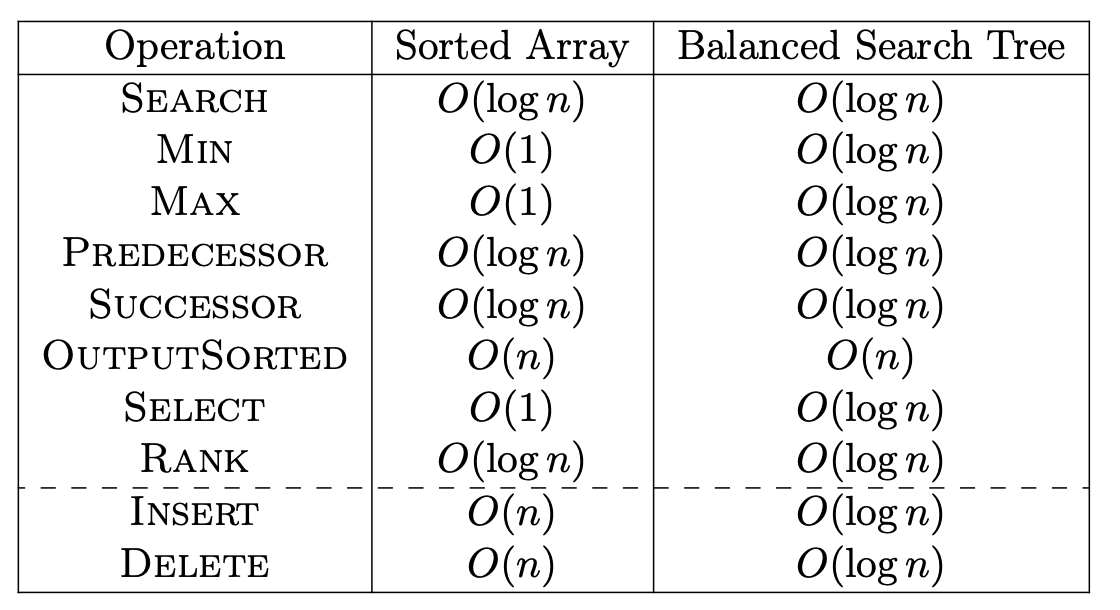
Important caveat: Above table are achieved by a balanced search tree. These running times are not guaranteed by an unbalanced search tree.
When to use a balanced search tree:
If you application requires maintaining an ordered representation of a dynamically changing set of objects, the balanced search tree is usually the data structure of choice.
import random
import time
def swap(array, a, b):
temp = array[a]
array[a] = array[b]
array[b] = temp
return array
def search_median(array, median, l, r):
# only in the number of odds
pivot = random.randint(l, r)
array = swap(array, pivot, l)
i = l + 1
for j in range(l + 1, r + 1):
if array[j] <= array[l]:
array = swap(array, i, j)
i = i + 1
array = swap(array, l, i - 1)
if i - 1 == median:
return array[i - 1]
elif i - 1 > median:
# left
return search_median(array, median, l, i - 2)
else:
# right
return search_median(array, median, i, r)
class SearchTree:
"""
Search Table Format as follows.
"""
def __init__(self, array):
# O(n) to find the median
median = int(len(array) / 2) - 1
self.root = search_median(array, median, 0, len(array) - 1)
array.remove(self.root)
# generate the initial tree
self.search_tree = []
self.search_tree.append([self.root, None, None, None])
while array:
item = array.pop()
self.insert(item)
def get_parent(self, node):
return self.search_tree[node][1]
def get_left_child(self, node):
return self.search_tree[node][2], 2
def get_right_child(self, node):
return self.search_tree[node][3], 3
def insert(self, item):
node = 0
parent = None
child = None
while node is not None:
value = self.search_tree[node][0]
parent = node
if item > value:
node, child = self.get_right_child(node)
else:
node, child = self.get_left_child(node)
# update the the record in the tree
self.search_tree.append([item, parent, None, None])
if parent is not None:
self.search_tree[parent][child] = len(self.search_tree) - 1
if __name__ == "__main__":
r = 1000000
array = [random.randint(0, r) for _ in range(r)]
tic = time.time()
SearchTree = SearchTree(array)
toc = time.time()
print(f"time elapse {toc - tic} s")
- You are given a binary tree with n nodes (via a pointer to its root). Each node of the tree has a size field, as in Section 11.3.9, but these fields have not been filled in yet. How much time is necessary and sufficient to compute the correct value for all the size fields?
Because every node should only be traversed once, so I think the total time is $\Theta(n)$. (unconfirmed yet)